Oni koji vole matematiku reći će da je ona lijepa zato što naizgled jednostavni obrasci vode do mnogo složenijih pitanja i teorija. Collatzova pretpostavka jedna je od takvih začkoljica koja matematičare uči još otkako je 1937. problem postavio matematičar Lothar Collatz, dvije godine nakon obrane doktorata.
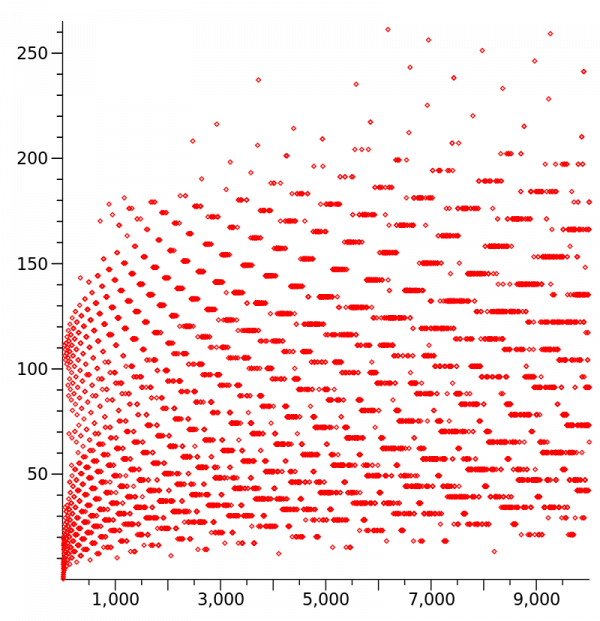
Godine i desetljeća prolaze, a matematičari i dalje ne znaju riješiti ovaj naizgled jednostavan problem. Suština je sljedeća: Izaberite bilo koji pozitivni cijeli broj. Podijelite ga s 2 ako je paran, ili pomnožite s 3 i dodate 1 ako je neparan. Ponovite ovaj postupak s dobivenim brojem... Na kraju ćete uvijek završiti s brojem 1.
Matematičari su isprobali milijune brojeva i nikad nisu pronašli nijedan koji se na kraju nije završio s 1. Stvar je u tome što oni nikad nisu uspjeli dokazati da ne postoji poseban broj koji nikad ne vodi do 1. Moguće je da postoji neki stvarno veliki broj koji ide u beskonačnost, ili možda broj koji se zaglavi u petlje i nikad ne dosegne 1. Ali to dosad nitko nije mogao dokazati sa sigurnošću.
Ako ne vjerujete, pogledajte ovaj video u kojem profesor David Eisenbud s kalifornijskog sveučilišta u Berkeleyu demonstrira postupak, također poznat i kao problem 3n + 1 , Ulamova pretpostavka, Kakutanijev problem, Hasseov algoritam i Sekvenca tuče, koristeći pritom brojku 7:
U međuvremenu, Collatzova pretpostavka ostaje tema mnogih rasprava, o tome je matematičkom problemu napisan barem jedan udžbenik i niz znanstvenih studija. Ostalo je zapisano i da je ugledni mađarski matematičar Paul Erdős bespomoćno izjavio: 'Matematika još nije spremna za takve probleme'.